Mesh/torus functions (coNCePTuaL User’s Guide)

Mesh/torus functions

coNCePTuaL provides three functions— MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE—that help treat (linear) task IDs as positions on a multidimensional mesh or torus. Each of these functions takes a variable number of arguments, determined by the dimensionality of the mesh (1-D, 2-D, or 3-D).

Terminology note: In the context of network topologies in general and MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE in particular, “torus” refers to a mesh topology, of any number of dimensions, that contains wraparound links. That is, nodes on the right side of the mesh are directly connected to nodes on the left side of the mesh, nodes on the top of the mesh are directly connected to nodes on the bottom of the mesh, and so forth. A “partial torus” refers to a mesh topology of two or more dimensions in which at least one dimension contains wraparound links and at least one dimension does not.

Function: MESH_NEIGHBOR (‘(’ width ‘*’? [, height ‘*’? [, depth ‘*’?]] ‘)’, task_ID, ‘(’ x_offset [, y_offset [, z_offset]] ‘)’): MESH_NEIGHBOR returns a task’s neighbor on a 1-D, 2-D, or 3-D mesh or torus. It takes exactly three arguments: a list of the mesh/torus’s dimensions, a task number, and a list of the neighbor’s offset in each dimension from the given task. The two list arguments must be parenthesized, even if they contain only a single element. Each dimension in the dimension list may be followed by an asterisk to indicate that the mesh wraps around in that dimension. If not specified, height and depth default to ‘1’, and y_offset and z_offset default to ‘0’. In the absence of wraparound links, offsets that move off the mesh cause MESH_NEIGHBOR to return the value ‘-1’.

Function: MESH_COORDINATE (‘(’ width ‘*’? [, height ‘*’? [, depth ‘*’?]] ‘)’, task_ID, coordinate): MESH_COORDINATE returns a task’s x, y, or z coordinate on a 1-D, 2-D, or 3-D mesh/torus. The first argument to MESH_COORDINATE is a list of the mesh/torus’s dimensions. The second argument is a task number. The third argument should be ‘0’ to calculate an x coordinate, ‘1’ to calculate a y coordinate, or ‘2’ to calculate a z coordinate. Coordinates are zero-origined. Each dimension in the dimension list may be followed by an asterisk to indicate that the mesh wraps around in that dimension, but this has no impact on the result. (Asterisks are allowed solely for consistency with the other mesh functions.)

Function: MESH_DISTANCE (‘(’ width ‘*’? [, height ‘*’? [, depth ‘*’?]] ‘)’, task_ID_1, task_ID_2): MESH_DISTANCE returns the shortest Manhattan distance between two tasks on a 1-D, 2-D, or 3-D mesh or torus. It takes exactly three arguments: a list of the mesh/torus’s dimensions and two task numbers. The list argument must be parenthesized, even if it contains only a single element. Each dimension in the dimension list may be followed by an asterisk to indicate that the mesh wraps around in that dimension. If not specified, height and depth default to ‘1’.

MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE number tasks following the right-hand rule: left-to-right, then top-to-bottom, and finally back-to-front, as shown in the following illustrations of a 4-element (1-D) mesh, a 4x3 (2-D) mesh, and a 4x3x2 (3-D) mesh. Examples of MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE for 1-D, 2-D, and 3-D meshes follow the corresponding illustration.

The following examples show how to use MESH_NEIGHBOR and MESH_COORDINATE to calculate neighbors and coordinates on the 1-D mesh shown above:

‘MESH_NEIGHBOR((4), 0, (-1))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4), 0, (+1))’ ⇒ ‘1’
‘MESH_NEIGHBOR((4), 1, (-1))’ ⇒ ‘0’
‘MESH_NEIGHBOR((4), 1, (+1))’ ⇒ ‘2’
‘MESH_NEIGHBOR((4), 2, (-1))’ ⇒ ‘1’
‘MESH_NEIGHBOR((4), 2, (+1))’ ⇒ ‘3’
‘MESH_NEIGHBOR((4), 3, (-1))’ ⇒ ‘2’
‘MESH_NEIGHBOR((4), 3, (+1))’ ⇒ ‘-1’
‘MESH_COORDINATE((4), -1, 0)’ ⇒ ‘-1’
‘MESH_COORDINATE((4), 0, 0)’ ⇒ ‘0’
‘MESH_COORDINATE((4), 1, 0)’ ⇒ ‘1’
‘MESH_COORDINATE((4), 2, 0)’ ⇒ ‘2’
‘MESH_COORDINATE((4), 3, 0)’ ⇒ ‘3’
‘MESH_COORDINATE((4), 4, 0)’ ⇒ ‘-1’
‘MESH_COORDINATE((4), 2, 1)’ ⇒ ‘0’
‘MESH_COORDINATE((4), 2, 2)’ ⇒ ‘0’
‘MESH_DISTANCE((4), -1, 0)’ ⇒ ‘-1’
‘MESH_DISTANCE((4), 1, 2)’ ⇒ ‘1’
‘MESH_DISTANCE((4), 0, 3)’ ⇒ ‘3’

We can treat the 1-D mesh as a 1-D torus (a ring) by putting a ‘*’ after the length of the x dimension:

‘MESH_NEIGHBOR((4*), 0, (-1))’ ⇒ ‘3’
‘MESH_NEIGHBOR((4*), 3, (+1))’ ⇒ ‘0’
‘MESH_DISTANCE((4*), -1, 0)’ ⇒ ‘-1’
‘MESH_DISTANCE((4*), 1, 2)’ ⇒ ‘1’
‘MESH_DISTANCE((4*), 0, 3)’ ⇒ ‘1’

The remaining MESH_NEIGHBOR examples return the same value as before. MESH_COORDINATE always returns the same value regardless of the presence or absence of wraparound links.

The next set of examples shows how to use MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE to calculate neighbors, coordinates, and distances on the 2-D mesh shown above:

‘MESH_NEIGHBOR((4, 3), 5, (-1, -1))’ ⇒ ‘0’
‘MESH_NEIGHBOR((4, 3), 5, ( 0, -1))’ ⇒ ‘1’
‘MESH_NEIGHBOR((4, 3), 5, (+1, -1))’ ⇒ ‘2’
‘MESH_NEIGHBOR((4, 3), 5, (-1, 0))’ ⇒ ‘4’
‘MESH_NEIGHBOR((4, 3), 5, ( 0, 0))’ ⇒ ‘5’
‘MESH_NEIGHBOR((4, 3), 5, (+1, 0))’ ⇒ ‘6’
‘MESH_NEIGHBOR((4, 3), 5, (-1, +1))’ ⇒ ‘8’
‘MESH_NEIGHBOR((4, 3), 5, ( 0, +1))’ ⇒ ‘9’
‘MESH_NEIGHBOR((4, 3), 5, (+1, +1))’ ⇒ ‘10’
‘MESH_COORDINATE((4, 3), 1, 0)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3), 6, 0)’ ⇒ ‘2’
‘MESH_COORDINATE((4, 3), 6, 1)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3), 6, 2)’ ⇒ ‘0’
‘MESH_COORDINATE((4, 3), 8, 0)’ ⇒ ‘0’
‘MESH_COORDINATE((4, 3), 8, 1)’ ⇒ ‘2’
‘MESH_COORDINATE((4, 3), 12, 0)’ ⇒ ‘-1’
‘MESH_DISTANCE((4, 3), 1, 2)’ ⇒ ‘1’
‘MESH_DISTANCE((4, 3), 2, 6)’ ⇒ ‘1’
‘MESH_DISTANCE((4, 3), 0, 5)’ ⇒ ‘2’
‘MESH_DISTANCE((4, 3), 3, 9)’ ⇒ ‘4’
‘MESH_DISTANCE((4, 3), 11, 0)’ ⇒ ‘5’

Wraparound links turn some out-of-bounds (‘-1’) neighbor values into in-bounds values and reduce some of the shortest-path distances between tasks:

‘MESH_NEIGHBOR((4, 3), 5, (-2, 0))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4, 3), 5, (-2, -2))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4, 3*), 5, (-2, 0))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4, 3*), 5, (-2, -2))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4*, 3), 5, (-2, 0))’ ⇒ ‘7’
‘MESH_NEIGHBOR((4*, 3), 5, (-2, -2))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4*, 3*), 5, (-2, 0))’ ⇒ ‘7’
‘MESH_NEIGHBOR((4*, 3*), 5, (-2, -2))’ ⇒ ‘11’
‘MESH_DISTANCE((4*, 3*), 1, 2)’ ⇒ ‘1’
‘MESH_DISTANCE((4*, 3*), 2, 6)’ ⇒ ‘1’
‘MESH_DISTANCE((4*, 3*), 0, 5)’ ⇒ ‘2’
‘MESH_DISTANCE((4*, 3*), 3, 9)’ ⇒ ‘3’
‘MESH_DISTANCE((4*, 3*), 11, 0)’ ⇒ ‘2’

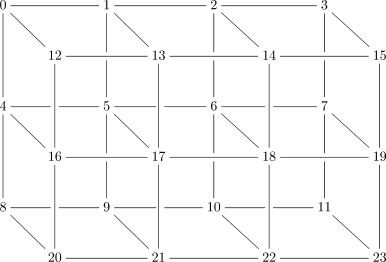
The final set of examples in this section shows how to use MESH_NEIGHBOR, MESH_COORDINATE, and MESH_DISTANCE to calculate neighbors, coordinates, and distances on the 3-D mesh shown above:

‘MESH_NEIGHBOR((4, 3, 2), 0, (0, 0, +1))’ ⇒ ‘12’
‘MESH_NEIGHBOR((4, 3, 2), 0, (0, +1, 0))’ ⇒ ‘4’
‘MESH_NEIGHBOR((4, 3, 2), 0, (+1, 0, 0))’ ⇒ ‘1’
‘MESH_NEIGHBOR((4, 3, 2), 0, (+1, +1, +1))’ ⇒ ‘17’
‘MESH_NEIGHBOR((4, 3, 2), 17, (+2, -1, -1))’ ⇒ ‘3’
‘MESH_NEIGHBOR((4, 3, 2), 23, (+1, +1, +1))’ ⇒ ‘-1’
‘MESH_NEIGHBOR((4, 3, 2), 7, (+100, -200, +300))’ ⇒ ‘-1’
‘MESH_COORDINATE((4, 3, 2), -5, 0)’ ⇒ ‘-1’
‘MESH_COORDINATE((4, 3, 2), 1, 0)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3, 2), 6, 0)’ ⇒ ‘2’
‘MESH_COORDINATE((4, 3, 2), 6, 1)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3, 2), 6, 2)’ ⇒ ‘0’
‘MESH_COORDINATE((4, 3, 2), 18, 0)’ ⇒ ‘2’
‘MESH_COORDINATE((4, 3, 2), 18, 1)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3, 2), 18, 2)’ ⇒ ‘1’
‘MESH_COORDINATE((4, 3, 2), 18, 3)’ ⇒ error→ Invalid coordinate
‘MESH_DISTANCE((4, 3, 2), 23, 24)’ ⇒ ‘-1’
‘MESH_DISTANCE((4, 3, 2), 5, 17)’ ⇒ ‘1’
‘MESH_DISTANCE((4, 3, 2), 1, 16)’ ⇒ ‘3’
‘MESH_DISTANCE((4, 3, 2), 14, 8)’ ⇒ ‘5’
‘MESH_DISTANCE((4, 3, 2), 0, 23)’ ⇒ ‘6’

As before, wraparound links affect some of the return values:

‘MESH_NEIGHBOR((4*, 3*, 2*), 23, (+1, +1, +1))’ ⇒ ‘0’
‘MESH_NEIGHBOR((4*, 3*, 2*), 7, (+100, -200, +300))’ ⇒ ‘11’
‘MESH_DISTANCE((4*, 3*, 2*), 23, 24)’ ⇒ ‘-1’
‘MESH_DISTANCE((4*, 3*, 2*), 5, 17)’ ⇒ ‘1’
‘MESH_DISTANCE((4*, 3*, 2*), 1, 16)’ ⇒ ‘3’
‘MESH_DISTANCE((4*, 3*, 2*), 14, 8)’ ⇒ ‘4’
‘MESH_DISTANCE((4*, 3*, 2*), 0, 23)’ ⇒ ‘3’

Scott Pakin, pakin@lanl.gov